L’univers de la publicité programmatique est vaste et complexe. Utiliser le terme « univers » n’est même pas suffisant pour le décrire. C’est une rivière sans fin qui s’écoule à la vitesse de la lumière. Un flux de données incessant ou les contraintes du temps n’existent pas.

Le marché de la publicité programmatique c’est un taux de croissance annuel de 22,8% de 2025 à 2030. C’est 984 milliards de dollars d’investissement prévue pour 2025. En d’autres termes, c’est un mastodonte. Cependant cet article n’a pas pour vocation d’énumérer les nombreuses tendances de cet univers si vaste, il a plutôt pour vocation de se pencher sur un des aspects les plus fascinants des DSP (Demand Side Platform) : le bid shading. C’est un des algorithmes parmi tant d’autres. Ceux présents dans les DSP sont si complexes qu’il ne serai pas exagéré de considérer les développeurs à l’origine comme des artistes. Des milliards de bid requests sont envoyées chaque jour il faut donc ordonner cet orchestre incessant.

Le bid shading s’inscrit dans la branche du RTB (Real Time Bidding), système d’enchères en temps réel. Car oui, le programmatique, ce n’est pas seulement du RTB. Cependant il est dans un premier temps nécessaire de rappeler sous quel modèle le marché fonctionne. En effet il fut un temps ou le second price auction rythmait les enchères. C’est aujourd’hui le first price auction.

First Price Auction ? Second Price Auction ?

Le first price auction consiste à payer l’impression au prix exact auquel nous avons biddé. C’est l’enchère la plus haute qui l’emporte.

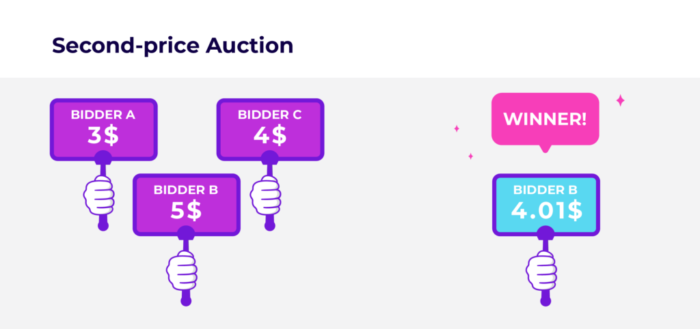
Supposons 3 potentiels acheteurs : Jean, Bernard et Roger. Jean est interessé, il bid à 3$. Bernard l’est aussi, il bid à 5$ et Roger est très intéressé, mais il bid à 4$.

Bernard à proposé l’offre la plus alléchante au vendeur, il remporte l’enchère.

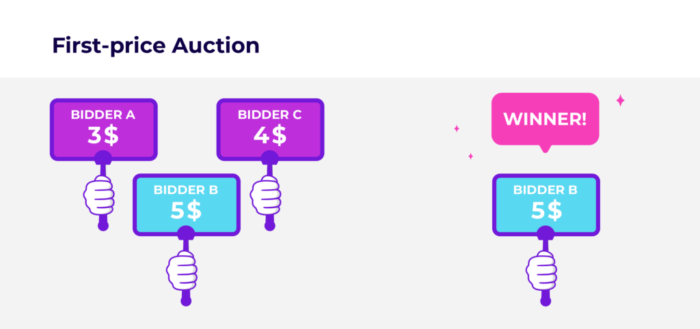
Le second price auction est légèrement différent mais le principe est similaire. L’enchère la plus haute l’emporte, mais l’acheteur ne va pas payer l’impression auquel il a biddé, il va la payer 1 centimes de plus que la deuxième meilleure enchère. Reprenons l’exemple précédent ou Bernard bid à 5$, il va remporte l’enchère mais ne va payer que 4,01$, soit un centime de plus.

Google a été le premier à abandonner ce modèle, les autres acteurs du marché ont suivi. En effet ce modèle à fait l’objet de nombreux problèmes notamment de transparence. Tels que :

• Des enchères au premier prix non déclarées comme telles
• L’utilisation de prix-planchers dynamiques
• La duplication des bid requests

Désormais, attardons-nous sur le vif du sujet, le bid shading. Comme évoqué précédemment, l’univers du RTB est concurrentiel et il faut donc pouvoir optimiser sa façon de bidder. C’est là ou les algorithmes des DSP entrent en jeu. En effet pour l’annonceur, il faut absolument éviter de surpayer l’enchère et le DSP est l& pour ça. Pour l’aider à payer au moins au juste prix. Dans cet article, c’est le modèle de bid shading de la plateforme « Xandr » qui sera expliqué car réputée pour avoir un algorithme de bid shading très agressif. On aurait tendance à croire que le modèle au First Price avantage les vendeurs et que le modèle au Second Price avantage les acheteurs mais ce n’est pas totalement vrai car les acheteurs auront plutôt tendance à baisser drastiquement leurs bids pour éviter de surpayer dans un modèle au First Price mais là n’est pas le sujet.

Ce qui permet au bid shading d’exister, ce sont les données et sa conservation. Les DSP vont enregistrer chaque enchère gagnante ayant eu lieu et vont la catégoriser, la ranger. Et le lendemain, le DSP adaptera son bid, en fonction du prix de la veille et de ses critères. Car oui, le bid shading traite différent critères.

Pour faire simple, l’algorithme est un élève, c’est un élève studieux qui apprend et le lendemain, il commettra une erreur de moins que la veille c’est à dire qu’il va envoyer un bid encore plus efficace que la veille, censer en théorie gagner l’impression à un prix plus bas que la veille. Ce qui est fascinant, c’est que le DSP étudie non seulement le contexte de l’enchère gagnante, mais il va également étudier la façon dont les autres enchérisseurs ont biddé. Lors d’enchères futures, l’algorithme adaptera son bid en fonction du contexte mais aussi en fonction des autres potentiels acheteurs et de leurs façons de procéder.

Le but est de trouver le bid « parfait ». Il n’est ni trop haut, ni trop bas, il sera au juste prix. Mais supposons que le DSP n’a aucune données passées à exploiter !

Prenons l’exemple de l’algorithme Xandr appelé BPO (Bid Price Optimisation). Voici les conditions que l’algorithme s’applique si aucune données précédentes n’est exploitables sur telle impression :

• L’acheteur commence par réduire de 20% son bid de l’estimation initiale.
• Si l’acheteur gagne l’enchère et n’a jamais perdu pour l’instant, le prochain bid sera réduit de 10% de l’estimation initiale.
• Si l’acheteur perd l’enchère pour la première fois, le prochain bid sera augmenté de 8% du dernier bid gagné.
• Si l’acheteur gagne l’enchère mais a perdu la précédente, le prochain bid sera réduit de 4% du dernier bid gagné.
• Si l’acheteur perd 2 fois de suite ou plus, le prochain bid sera augmenté de 10% minimum mais peut être augmenté de 99% de l’estimation initiale au maximum.

Voici pour illustration un tableau issu de la documentation Xandr, qui démontre comment s’est déroulé 7 manches d’enchères entre deux acheteurs qui adoptaient le modèle algorithmique énoncé ci-dessus.

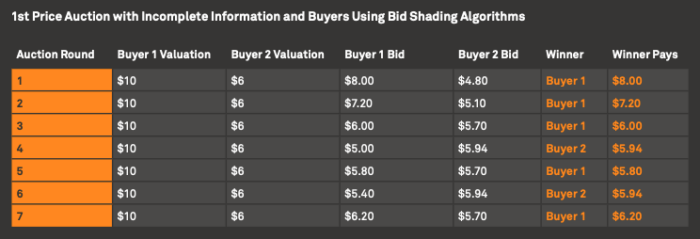
Évidemment ce qui est appelé « valuation » peut être considéré comme le prix de base que ce fixe le DSP, il dépend de nombreuses conditions notamment du budget total attribué sur une période.

En d’autres termes, cette optimisation est devenu indispensable pour les acheteurs notamment depuis le passage au first-price. Désormais, les algorithmes sont encore plus poussés qu’auparavant, notamment grâce à l’IA. C’est le cas de The Trade Desk, l’un des principaux si ce n’est le principal acteur du marché.

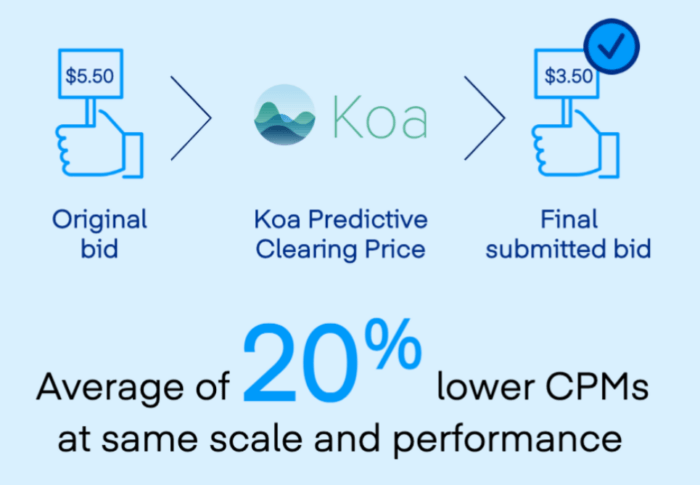
Son IA « Koa » analyse précisément le ou les historiques d’achats et adapte un bid proche de l’idéal. C’est ce que The Trade Desk appelle le « Predictive Clearing Optimization ».